Question

a rational function with at least one vertical asymptote, and a horizontal asymptote. You will describe the characteristics of your function, and give a numerical example of the function at one of the vertical asymptotes.

Answer 1

ANSWERS

Function:

`h(x)=(x+1)/((x-1)(x+3))`

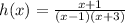
Key features:

• Asymptotes: x = 1, x = -3, (vertical), and ,y = 0, (horizontal).

,

• Intercepts: (0, -1/3), (-1, 0)

,

• Symmetry: none

,

• Example of end behavior: as x → 1⁺, y → infinity,, while, as x → 1⁻, y → -infinity

Step-by-step explanation

The vertical asymptotes of a rational function are given by the zeros of the denominator. For example, the function,

`h(x)=(x+1)/((x-1)(x+3))`

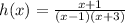
Has two vertical asymptotes: one at x = 1, and one at x = -3.

The horizontal asymptote is determined by the degrees of the numerator (n) and denominator (m):

• If n < m then the horizontal asymptote is the x-axis

,

• If n = m then the horizontal asymptote is y = a/b, where a and b are the leading coefficients of the numerator and denominator, respectively.

,

• If n > m then there is no horizontal asymptote

In the given example, the degree of the numerator is 1, while the degree of the denominator is 2. Thus, function h(x) has a horizontal asymptote that is the x-axis.

Now, we have to find the key features for this function:

• y-intercept:, occurs when x = 0

`h(0)=(0+1)/((0-1)(0+3))=(1)/(-3)=-(1)/(3)`

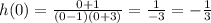
Hence, the y-intercept is (0, -1/3)

• x-intercepts:, the x-intercepts are the x-intercepts of the numerator: ,(-1, 0),.

,

• The ,asymptotes, are the ones mentioned above: ,x = 1, x = -3, (vertical), and ,y = 0, (horizontal).

,

• The ,symmetry, is determined as follows:

`\begin{gathered} Even\text{ }functions:f(-x)=f(x) \\ Odd\text{ }functions:f(-x)=-f(x) \end{gathered}`

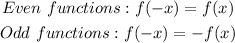
If we replace x with -x in function h(x), we will find that the result is neither h(x) nor -h(x) and, therefore this function is neither even nor odd.

Finally, an example of the end behavior of this function around the asymptote x = 1 is that as x → 1⁺, y → infinity, while as x → 1⁻¹, y → -infinity.

If we take values of x greater than x = 1 - so we will approach 1 from the right, we will get values of the function that show an increasing behavior. Let's find h(x) for x = 4, x = 3, and x = 2,

`\begin{gathered} h(4)=(4+1)/((4-1)(4+3))=(5)/(3\cdot7)=(5)/(21) \\ \\ h(3)=(3+1)/((3-1)(3+3))=(4)/(2*6)=(4)/(12)=(1)/(3) \\ \\ h(2)=(2+1)/((2-1)(2+3))=(3)/(1*5)=(3)/(5) \end{gathered}`

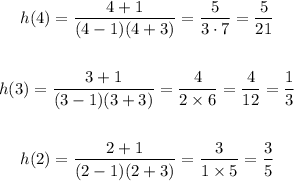
And we will find the opposite behavior for values that are less than 1 - but greater than -1 because there the function has a zero and its behavior could change,

`\begin{gathered} h(0)=(0+1)/((0-1)(0+3))=(1)/(-1*3)=-(1)/(3) \\ \\ h((1)/(2))=((1)/(2)+1)/(((1)/(2)-1)((1)/(2)+3))=((3)/(2))/(-(1)/(2)*(7)/(2))=((3)/(2))/(-(7)/(4))=-(3\cdot4)/(2\cdot7)=-(6)/(7) \end{gathered}`

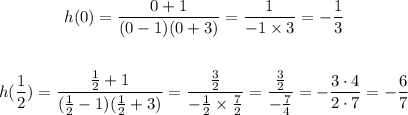
The graph of the function and its key features is,