We are given two lengths of the rectangle:
RU=3x-6
UT=x+9
These two lengths are shown in the following diagram:
Since this is a rectangle, the lengths of RU and UT must be equal:
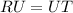
Thus
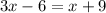
We need to solve this equation for x.
We start by subtracting x to both sides of the equation:
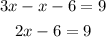
Now, add 6 to both sides:
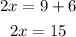
Finally, divide both sides by 2:
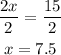
We have the value of x: x=7.5
Now we have to find the length of QS. Since QS and RT are diagonals of the same rectangle, they have to be equal:
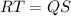
This means that we can find RT by adding RU and UT, and the result will be equal to QS:
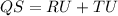
substituting the given expressions for RU and TU:

And now, substitute x=7.5 and solve for QS:
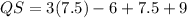
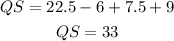
Answer:
x=7.5 and QS=33