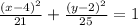Question

Find an equation for the ellipse whose vertices are at (4,-3) and (4,7), and focus is at (4,4).

Answer 1

The vertices of the ellipse are given as

`\begin{gathered} V_2=(4,-3) \\ V_1=(4,7) \end{gathered}`

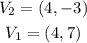
The focus of the ellipse is given as

`(4,4)`

The equation of an ellipse is given as

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

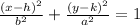
Where the coordinate of the center is

`(h,k)`

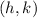
To calculate the coordinate of the center, we will use the formula below

`\begin{gathered} ((x_1+x_2))/(2),((y_1+y_2))/(2) \\ =((4+4))/(2),((-3+7))/(2) \\ =(8)/(2),(4)/(2) \\ (4,2) \\ (h,k)=(4,2) \end{gathered}`

The formula to calculate the value of a is given below

`\begin{gathered} V_1=(h,k+a) \\ V_2=(h,k-a) \end{gathered}`

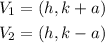
By comparing coefficients, we will have

`\begin{gathered} k+a=7\ldots\text{.}(1) \\ k-a=-3\ldots\text{.}(2) \end{gathered}`

By adding equations (1) and (2) and solving simultaneously, we will have

`\begin{gathered} 2k=4 \\ \text{divide both sides by 2,} \\ (2k)/(2)=(4)/(2) \\ k=2 \end{gathered}`

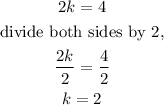
By substituting hk=2 in equation 1, we will have

`\begin{gathered} k+a=7 \\ 2+a=7 \\ a=7-2 \\ a=5 \end{gathered}`

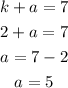
The coordinate of the focus,is calculated using the formula below

`(h,k+c)`

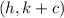
By substituting the values, we will have

`\begin{gathered} k+c=4 \\ 2+c=4 \\ c=4-2 \\ c=2 \end{gathered}`

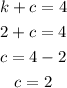
The value of will be calculated using the formula below

`\begin{gathered} c^2=a^2-b^2 \\ b^2=a^2-c^2 \end{gathered}`

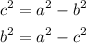
By substituting the values, we will have

`\begin{gathered} b^2=a^2-c^2 \\ b^2=(5)^2-(2^2 \\ b^2=25-4 \\ b^2=21 \end{gathered}`

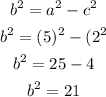
By substituting the values of a,b,h and k in the equation of an ellipse, we will have

`\begin{gathered} ((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1 \\ \frac{(x-4)^2}{21^{}}+\frac{(y-2)^2}{25^{}}=1 \\ \end{gathered}`

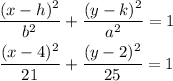
Hence,

The equation of the ellipse will be

`\frac{(x-4)^2}{21^{}}+\frac{(y-2)^2}{25^{}}=1`