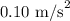Question

A car, initially traveling at 2.0 miles per hour, comes to rest in 8.6 s. What was its acceleration in this time?

Answer 1

Given:

the speed of the car is

`u=2.0\text{ mi/h}`

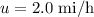
Time during which it comes to rest

`t=8.6\text{ s}`

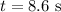
Required: acceleration is to be calculated

Explanation:

first, convert the speed from miles per hour to meters per second

in doing so we use a conversion factor

that is given as

`1\text{ mi/h= 0.447 m/s}`

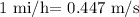
Then the speed is ,

`\begin{gathered} u=2.0\text{ }*0.447 \\ u=0.894\text{ m/s} \end{gathered}`

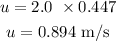
now calculate the acceleration,

we know that

`v=u+at`

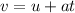
where v is the final velocity that is zero because finally, the car comes to rest.

plugging all the values in the above relation, we get

`\begin{gathered} 0=0.894\text{ m/s }+a*8.6\text{ s} \\ a=-(0.894)/(8.6) \\ a=-0.10\text{ m/s}^2 \end{gathered}`

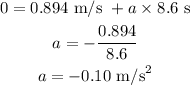
negative sign shows that acceleration in the opposite direction

Thus, the acceleration is

`0.10\text{ m/s}^2`