Let the width of the field = w
∵ The length is four times as the width
∵ The width = w
∴ The length = 4w
∵ The length is decreased by 10 feet
∴ The new length = 4w - 10
∵ The width is increased by 2 feet
∴ The new width = w + 2
The new perimeter is 80 feet
∵ The perimeter of the rectangle = 2(length + width)
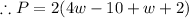
Let us simplify it
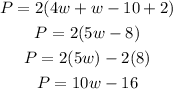
Now equate it by 80
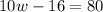
Add 16 to both sides
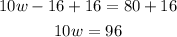
Divide both sides by 10

The length is 4 times the width

The length is 38.4 feet and the width is 9.6 feet