Question

A 1-cm high object is placed 10 cm in front of a concave mirror with a focal length 15 cm. Determine the image distance and the magnification. Enumerate the characteristics of the image produced. Must follow GRESA format.Given:Required:Equation(s) Needed:Solution:(a)(b)(c)Final answer:L-ocationO-rientation:S-izeT-ype:

Answer 1

Given:

object size: 1 cm

object distance (do): 10 cm

mirror focal length (f): 15 cm

Required:

Image distance (di),

magnification

image characteristics.

Equations needed:

`\begin{gathered} (1)/(d_i)+(1)/(d_o)=(1)/(f) \\ \text{magnification}=-(d_i)/(d_o) \end{gathered}`

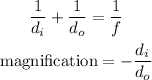
Solution:

`\begin{gathered} (1)/(d_i)+(1)/(10)=(1)/(15) \\ (1)/(d_i)=(1)/(15)-(1)/(10) \\ (1)/(d_i)=(2)/(30)-(3)/(30) \\ (1)/(d_i)=(-1)/(30)_{} \\ d_i=-30\text{ cm} \\ \\ \text{magnification}=-(-30)/(10)=3 \end{gathered}`

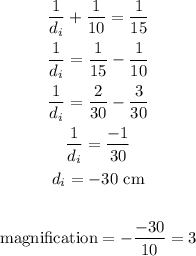
Location: 30 cm "inside" the mirror (di = -30)

Orientation: Upright (magnification > 0)

Size: 3 cm (object size multiplied by magnification)

Type: virtual image (di < 0)