Question

Solve the following system of linear equations using elimination. -3x + 3y=-3 2x-y=0

Answer 1

The system of equations is

`\begin{gathered} -3x+3y=-3\Rightarrow(1) \\ 2x-y=0\Rightarrow(2) \end{gathered}`

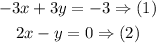
Since all terms in equation 1 can divide by 3, then

Divide each term in equation 1 by 3

`\begin{gathered} (-3x)/(3)+(3y)/(3)=(-3)/(3) \\ -x+y=-1\Rightarrow(3) \end{gathered}`

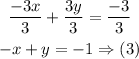
Add equations (2) and (3) to eliminate y

`\begin{gathered} (2x-x)+(-y+y)=(0-1) \\ x+0=-1 \\ x=-1 \end{gathered}`

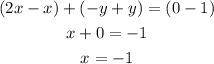
Substitute x by -1 in equation (2) to find y

`\begin{gathered} 2(-1)-y=0 \\ -2-y=0 \end{gathered}`

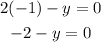
Add y to both sides

`\begin{gathered} -2-y+y=0+y \\ -2+0=y \\ -2=y \\ y=-2 \end{gathered}`

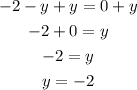
The solution of the given system of equations is (-1, -2)