Solution:
Given:
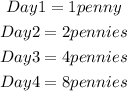
An exponential function is of the form:
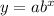
To get the exponential function for the relation;

Part A:
Relating this to the parameters given:
The exponential function that models the problem is;
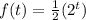
Part B:
On the twenty-third day,
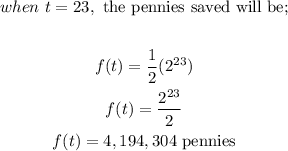
Therefore, he would have saved 4,194,304 pennies on the twenty-third day.