Question

Write the equation of the line that is perpendicular to the line 8y−16=5x through the point (5,-5).A. y=5/8x+3B. y=−8/5x−3C. y=−8/5x+3D. y=8/5x+3

Answer 1

Given the equation of the line below,

`8y-16=5x`

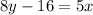
If the line passes through the point,

`(5,-5)`

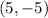
Re-writing the eqaution of the line in slope intercept form,

`\begin{gathered} 8y-16=5x \\ 8y=5x+16 \\ \text{Divide both sides by 8} \\ y=(5x)/(8)+(16)/(2) \\ y=(5)/(8)x+2 \end{gathered}`

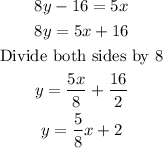
The slope of the perpendicular line is the negative reciprocal of the slope of the eqaution of the line in the slope-intercept form given above

The general form of the slope-intercept form of the equation of a straight line is,

`\begin{gathered} y=mx+c \\ \text{Where m is the slope} \\ y=(5)/(8)x+2 \\ m=(5)/(8) \\ \text{Slope of the perpendicular line is} \\ m_1=-(1)/(m) \\ m_{1_{}}=-(1)/((5)/(8))=-1*(8)/(5)=-(8)/(5) \end{gathered}`

The formula to find the equation of a line with point (5, -5) below is,

`\begin{gathered} (y-y_1)/(x-x_1)=m_1 \\ \text{Where} \\ (x_1,y_1)=(5,-5) \\ m_1=-(8)/(5) \end{gathered}`

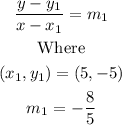
Substitute the values into the formula of the eqaution of a straight line,

`\begin{gathered} (y-(-5))/(x-5)=-(8)/(5) \\ (y+5)/(x-5)=-(8)/(5) \\ \text{Crossmultiply} \\ 5(y+5)=-8(x-5) \\ 5y+25=-8x+40 \\ \text{Collect like terms} \\ 5y=-8x+40-25 \\ 5y=-8x+15 \\ \text{Divide both sides by 5} \\ (5y)/(5)=-(8)/(5)x+(15)/(5) \\ y=-(8)/(5)x+3 \end{gathered}`

Hence, the right option is C