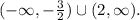Question

Solve each inequality). 2|4t-1|+6>20

Answer 1

To answer this question we will use the following property:

`|a|>b>0\text{ if and only if }a>b\text{ or }a<-b.`

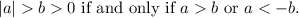
Subtracting 6 from the given inequality we get:

`\begin{gathered} 2|4t-1|+6-6>20-6, \\ 2|4t-1|>14. \end{gathered}`

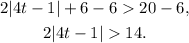
Dividing the above inequality by 2 we get:

`\begin{gathered} (2|4t-1|)/(2)>(14)/(2), \\ |4t-1|>7. \end{gathered}`

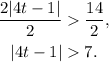
Then:

`4t-1>7\text{ or }4t-1<-7.`

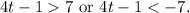
Solving the above inequalities we get:

1)

`4t-1>7.`

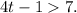
Adding 1 to the above inequality we get:

`\begin{gathered} 4t-1+1>7+1, \\ 4t>8. \end{gathered}`

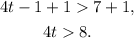
Dividing the above by 4 we get:

`\begin{gathered} (4t)/(4)>(8)/(4), \\ t>2. \end{gathered}`

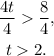
The above inequality in interval notation is:

`(2,\infty).`

2)

`4t-1<-7.`

Adding 1 to the above inequality we get:

`\begin{gathered} 4t-1+1<-7+1, \\ 4t<-6. \end{gathered}`

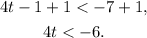
Dividing the above result by 4 we get:

`\begin{gathered} (4t)/(4)<-(6)/(4), \\ t<-(3)/(2). \end{gathered}`

The above inequality in interval notation is:

`(-\infty,-(3)/(2)).`

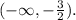
Answer:

`(-\infty,-(3)/(2))\cup(2,\infty).`