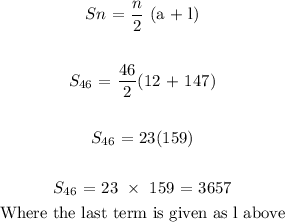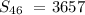
Here, we want to find the sum of the first 46 terms of the series
Here, what we have is a series with a first term of 12 and a common difference of 15-12=18-15 = 3
Before we proceed to get the sum of the first 46 terms, we can calculate the last term
The last term is given as;
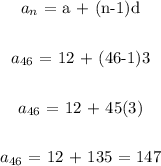
Now, we can apply the formula to get the sum
The formula is given as;