To answer this question, we need to know that we can represent, algebraically, two consecutive positive odd numbers as follows:

Then, if we have that the product of both consecutive positive odd numbers is 323, then:
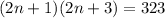
Now, we will need to expand the formula as follows:
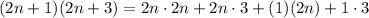
We applied the FOIL method to expand the expression. Then, we have:

Now, we have:
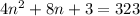

We have here a polynomial (a quadratic equation) that we can solve using the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},ax^2+bx+c=0](https://img.qammunity.org/2023/formulas/mathematics/college/d8qkmmh3mxtoovm8j5ja34n7ks11xlfyof.png)
Then, we have that:
• a = 4
,
• b = 8
,
• c = -320
Then
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\Rightarrow x=\frac{-8\pm\sqrt[]{8^2-4(4)(-320)}}{2\cdot4}](https://img.qammunity.org/2023/formulas/mathematics/college/41isgkvfsapxpt2xxn80b9gqp2xc5cret3.png)
![\Rightarrow x=\frac{-8\pm\sqrt[]{64^{}-4(4)(-320)}}{2\cdot4}\Rightarrow x=\frac{-8\pm\sqrt[]{64+5120}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/ea3cxhi9qcoph3x7odu2etwy0jxr0luea2.png)
![x=\frac{-8\pm\sqrt[]{5184}}{8}\Rightarrow x=(-8\pm72)/(8)](https://img.qammunity.org/2023/formulas/mathematics/college/98ptaktpsc42c48y8yphr27kanyt54hpi1.png)
Then, the solutions are:
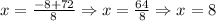
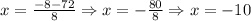
Therefore, we have two solutions for n, n = 8 or n = -10.
If we substitute the value of n = 8 in the original equations, we have:
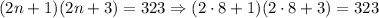
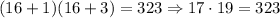
If we use the negative value for the solution, we obtain:
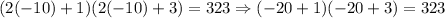
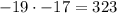
Since these two numbers are negative, we have that the appropriate solution is n = 8.
Therefore, we have that the smaller of the two numbers is 17:

The numbers 17 and 19 are consecutive positive odd numbers.
In summary, we have that the smaller number is 17.