Question

Find the value of k so that the remainder is 3(x^2-x+k) divided by (x-1)

Answer 1

Okay, here we have this:

Considering the provided polynomials, we are going to calculate the requested value, so we obtain the following:

So first we will perform the division assuming that k=0 to see what is the remainder that is obtained:

`\begin{gathered} (x^2-x)/(x-1) \\ =(x(x-1))/(x-1) \\ =x \end{gathered}`

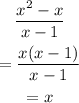
We obtain that the remainder when taking k=0, is zero, then it will mean that the k must be equal to the residue that we want:

In other words, if we want the remainder to be 3, k must be equal to 3, replacing:

`\begin{gathered} (x^2-x+k)/(x-1) \\ (x^2-x+3)/(x-1) \\ =x+(3)/(x-1) \end{gathered}`

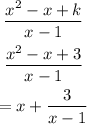
Finally we confirm that for the remainder to be 3, the value of k must be equal to 3.