Question

I need help with getting to the answer to number 6

Answer 1

Step-by-step explanation

We have the following pair of functions:

`\begin{gathered} f(x)=x^3+6x \\ g(x)=√(8x) \end{gathered}`

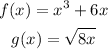
And we need to find (fog)(2). In order to do this we can start by calculating the composite function (fog)(x)=f(g(x)). Its expression is given by taking the equation of f(x) and replacing x with the expression of g(x). Then we get:

`\begin{gathered} (f\circ g)(x)=f(g(x))=g(x)^3+6g(x)=(√(8x))^3+6√(8x) \\ (f\circ g)(x)=(√(8x))^3+6√(8x) \end{gathered}`

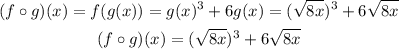
We need to find (fog)(2) so we just need to take x=2 in the equation above:

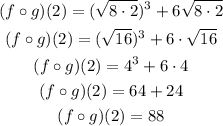
`\begin{gathered} (f\circ g)(2)=(√(8\cdot2))^3+6√(8\cdot2) \\ (f\circ g)(2)=(√(16))^3+6\cdot√(16) \\ (f\circ g)(2)=4^3+6\cdot4 \\ (f\circ g)(2)=64+24 \\ (f\circ g)(2)=88 \end{gathered}`Answer

Then the answer is 88.