Question

A line is graphed on the coordinate plane below.Line y = -2 +2 will be graphed on the same coordinate plane to create a system of equations.What is the solution to that system of equations?4A (-2,4)B (0-4)C (2,-4)0 (4,-2)Rod End TeeFlagOptionsBackNext

Answer 1

Step 1: Find the equation of the line in the graph.

Two points the line pass through are (0, -4) and (2, -3)

Thus,

`\begin{gathered} x_1=0,y_1=-4 \\ x_2=2,y_2=-3 \end{gathered}`
`\begin{gathered} The\text{ equation of the line can be calculated with the formula} \\ (y_2-y_1)/(x_2-x_1)=(y-y_1)/(x-x_1) \\ \\ (-3-(-4))/(2-0)=(y-(-4))/(x-0) \\ \\ (-3+4)/(2)=(y+4)/(x) \\ (1)/(2)=(y+4)/(x) \end{gathered}`
`\begin{gathered} 2(y+4)=x \\ 2y+8=x \\ 2y=x-8 \end{gathered}`

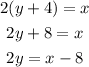
The equation of the graph is 2y = x - 8

Step 2:

Solve the two equations simultaneously to detemine the solution to the systems of equations

2y = x - 8 ------------------------equation (1)

y = -x + 2 ----------------------equation (2)

Add both equations to eliminate x

2y + y = x - 8 + (-x) + 2

3y = x -8-x+2

3y = -8 + 2

3y = -6

y = -6/3

y = -2

Substitute y = -2 into equation (2)

y = -x + 2

-2 = -x + 2

-2 -2 = -x

-4 = -x

-x = -4

Divide both sides by -1

x = 4

Hence, the solution to the system of equations is (4, -2)

The correct option is option D