Answer:
12 years
Explanation:
For an investment whose interest is compounded continuously, the amount in the account after t years is determined using the formula:
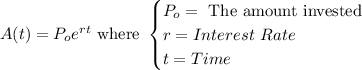
In our given problem:
• A(t) = $6,000
,
• Po = $4000
,
• r = 3.5% = 0.035
We want to find the value of t.
Substitute the given values into the formula:
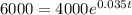
Then solve for t:
![\begin{gathered} \text{ Divide both sides by 4000} \\ (6000)/(4000)=(4000e^(0.035t))/(4000) \\ 1.5=e^(0.035t) \\ \text{ Take the ln of both sides:} \\ \ln(1.5)=\ln(e^(0.035t)) \\ 0.035t=\ln(1.5) \\ \text{ Divide both sides by }0.035 \\ (0.035t)/(0.035)=\frac{\operatorname{\ln}(1.5)}{0.035} \\ t=11.58 \\ t\approx12\text{ years} \end{gathered}]()
It will take Dennis 12 years (rounded to the nearest year) before he has $6,000 in his account.