Question

Scale the rectangle by finding 3A. What are the vertices of the scaled rectangle

Answer 1

Given A, the matrix that contains the vertices of a rectangle on the plane, calculate 3A as shown below

`3A=3\begin{bmatrix}{1} & {6} & {6} & {1} \\ {1} & {1} & {5} & {5} \\ {} & {} & {} & {} \\ {} & {} & {} & {}\end{bmatrix}=\begin{bmatrix}{3*1} & {3*6} & {3*6} & {3*1} \\ {3*1} & {3*1} & {3*5} & {3*5} \\ {} & {} & {} & {} \\ {} & {} & {} & {}\end{bmatrix}=\begin{bmatrix}{3} & {18} & {18} & {3} \\ {3} & {3} & {15} & {15} \\ {} & {} & {} & {} \\ {} & {} & {} & {}\end{bmatrix}`

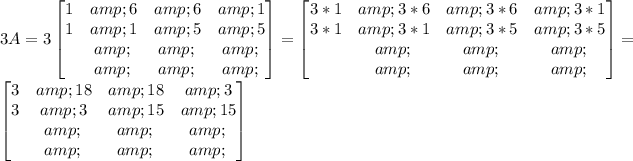
Where each column of the 4x2 matrix above represents a vertex of the new rectangle; therefore, the 4 vertices are

(3,3), (18,3), (18,15), (3,15). The second option.