Question

Find the real solution(s), if any, of the system by examining the graph

Answer 1

Given:

`\begin{gathered} -6x-3y=18\ldots\ldots\ldots(1) \\ (x^(2))/(9)+(y^(2))/(36)=1\ldots\ldots\ldots\ldots(2) \end{gathered}`

Let us consider the equation (1),

`\begin{gathered} -6x-3y=18 \\ -2x-y=6 \\ -y=2x+6 \\ y=-(2x+6)\ldots\ldots\ldots(3) \end{gathered}`

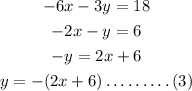
Substitute equation (3) in (2), we get

`\begin{gathered} (x^2)/(9)+\frac{(-(2x+6))^2_{}}{36}=1 \\ (4x^2)/(36)+(4x^2+36+24x)/(36)=1 \\ (4x^2+4x^2+36+24x)/(36)=1 \\ 8x^2+36+24x=36 \\ 8x^2+24x=0 \\ 8x(x+3)=0 \\ x=0,x=-3 \end{gathered}`

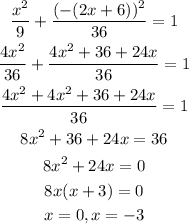
Substitute x=0 and x=-3 in equation (3) we get,

`\begin{gathered} y=-(2(0)+6) \\ =-6 \\ y=-(2(-3)+6) \\ =0 \end{gathered}`

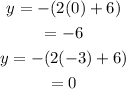
Hence, the solutions are, (0,-6) and (-3,0).

Let us verify this, by substituting (0,-6) and (-3,0) in equation (1), we get

For (0, -6),

`\begin{gathered} -6(0)-3(-6)=18 \\ 18=18 \end{gathered}`

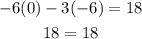
For (-3, 0)

`\begin{gathered} -6(-3)-3(0)=18 \\ 18=18 \end{gathered}`

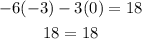
Hence, it is verified.