Question

Don’t get part ii of this question ? I needed help with this, please help me as I am confused.

Answer 1

We are given the following function:

`y=(1-10x)/((2x-1)^5)`

We are asked to differentiate with respect to "x". To do that we need to have into account that the function is rational and therefore, we need to use the quotient rule for derivatives, which is the following:

`(d)/(dx)((f(x))/(g(x)))=(f^(\prime)(x)g(x)-f(x)g^(\prime)(x))/(g^2(x))`

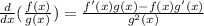
Therefore, we need to determine the derivatives of f(x) and g(x). In this case, we have:

`\begin{gathered} f(x)=1-10x \\ g(x)=(2x-1)^5 \end{gathered}`

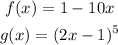
Now, we determine the derivative of f(x):

`(d)/(dx)(f(x))=(d)/(dx)(1-10x)`

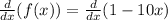
First, we distribute the derivative:

`(d)/(dx)(f(x))=(d)/(dx)(1)-(d)/(dx)(10x)`

The first, derivative is the derivative of a constant and therefore is zero:

`(d)/(dx)(f(x))=-(d)/(dx)(10x)`

For the second derivative we use the following rule:

`(d)/(dx)(ax)=a`

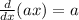
Applying the rule we get:

`(d)/(dx)(f(x))=-10`

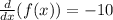
Therefore:

`f^(\prime)(x)=-10`

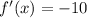
Now, we determine the derivative of g(x):

`(d)/(dx)(g(x))=(d)/(dx)(2x-1)^5`

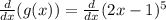
Now, we determine the derivative using the following rule:

`(d)/(dx)(g(x))^n=n(g(x))^(n-1)(g^(\prime)(x))`

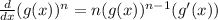
Applying the rule we get:

`(d)/(dx)(g(x))=5(2x-1)^4(2)`

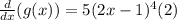
Simplifying:

`(d)/(dx)(g(x))=10(2x-1)^4`

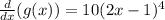
Therefore, we have:

`g^(\prime)(x)=10(2x-1)^4`

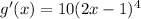
Now, we substitute the function in the quotient rule:

`(d)/(dx)((1-10x)/((2x-1)^5))=((-10)(2x-1)^5-(1-10x)(10)(2x-1)^4)/(((2x-1)^5)^2)`

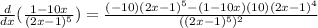
Now we simplify the denominator:

`(d)/(dx)((1-10x)/((2x-1)^5))=((-10)(2x-1)^5-(1-10x)(10)(2x-1)^4)/((2x-1)^(10))`

Now, we take (2x - 1)^4 as a common factor on the numerator:

`(d)/(dx)((1-10x)/((2x-1)^5))=\frac{(2x-1)^4((-10)(2x-1)^{}-(1-10x)(10))}{(2x-1)^(10)}`

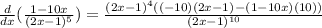
Now, we simplify the function:

`(d)/(dx)((1-10x)/((2x-1)^5))=\frac{((-10)(2x-1)^{}-(1-10x)(10))}{(2x-1)^6}`

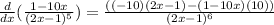
Now, we apply the distributive property on the numerator:

`(d)/(dx)((1-10x)/((2x-1)^5))=\frac{-20x+10^{}-10+100x}{(2x-1)^6}`

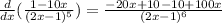
Now, we cancel out the 10 and add like terms:

`(d)/(dx)((1-10x)/((2x-1)^5))=(80x)/((2x-1)^6)`

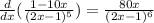
Since we can't simplify any further this is the final answer.