Question

One number is chosen from the list 2,4,6, and 8. Another is selected from the list 6, 7 and 8. Find the probability that they are the same. a. 0 b.1/6 c. 2/3 d. 1/3

Answer 1

There are 2 options to get the same number, they choose 6 from both lists or they choose 8 from both lists.

Then, the probability to select 6 from the first list is:

`(1)/(4)`

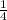
Because we have 4 options ( 2, 4, 6, 8) and 1 of then is number 6. At the same way, the probability to select 6 from the second list is:

`(1)/(3)`

Because there are 3 numbers and one of them is 6.

Finally, the probability to choose 6 from both lists is the multiplication of the probabilities above, so:

`P_6=(1)/(4)\cdot(1)/(3)=(1)/(12)`

We can also calculate the probability to choose 8 from both lists as:

`P_8=(1)/(4)\cdot(1)/(3)=(1)/(12)`

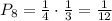
Because 1/4 is the probability to choose 8 from the first list and 1/3 is the probability to select 8 from the second list.

Therefore, the probability that both numbers are the same is the sum of the probability to choose 6 from both lists and the probability to choose 8 form both lists.

`\begin{gathered} P=P_6+P_8 \\ P=(1)/(12)+(1)/(12) \\ P=(1)/(6) \end{gathered}`

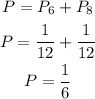
Answer: b. 1/6