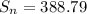Question

1. find the sum of the first 7 terms of the following sequence round to the nearest hundredth if necessary 18,-6,22. Find the sum of the first 6 terms of the following sequence to the nearest hundredth:324, 54, 9

Answer 1

You can find the sum of the first n terms of a geometric sequence using the formula:

`S_n=(a_1(1-r^n))/(1-r)`

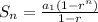
1. First, let's calculate r:

`\begin{gathered} r_1=18-(-6)=24 \\ r_2=-6-2=-8 \\ r=-(8)/(24)=-(1)/(3) \end{gathered}`

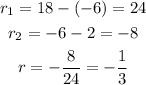
Replacing the values in the formula, (n=7 , r=-1/3) we get that:

`S_n=13.51`

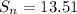
2. Let's calculate r:

`\begin{gathered} r_1=324-54=270 \\ r_2=54-9=45 \\ r=(r_2)/(r_1)=(45)/(270)=(1)/(6) \end{gathered}`

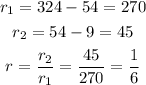
Using the formula with the data we have, (n=6 , r=1/6) we get that

`S_n=388.79`