Question

The volume of gas v held at a constant temperature in a closed container varies inversely with it's pressure P. If the V of gas is 1600 cm^3 when the P is 250 mm Hg, find the v when the P is 400 mm Hg?

Answer 1

`1000\text{ cm}^3`

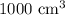
Step-by-step explanation

The volume of gas v held at a constant temperature in a closed container varies inversely with it's pressure P,in math terms it is

`\begin{gathered} V\propto(1)/(P) \\ where\text{ V is the volume} \\ P\text{ is the presion} \end{gathered}`

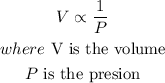
When Pressure is constant, Volume is directly proportional to temperature.

Step 1

given the data, we need to apply the formula for a constant temperature ,

`\begin{gathered} V_2=(P_1V_1T_2)/(T_1P_2) \\ as\text{ the temperature is constatn} \\ V_2=(P_1V_1)/(P_2) \end{gathered}`

so

`\begin{gathered} V_2=\frac{250\text{ mmHg*1600 cm}}{400} \\ V_2=1000\text{ cm}^3 \end{gathered}`

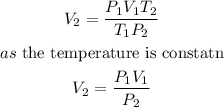
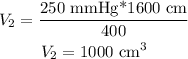
so, the answer is

`1000\text{ cm}^3`

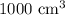
I hope this helps you