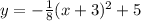Question

1v=9. Which equation represents the equation of theparabola with focus (-3,3) and directrix y = 7?A),= (x+3)2 – 5B) y = 5(? – 3)2 +5C) y=-( + 3)2 +5D) y=-2 (2-3)2 +5

Answer 1

From the focus (-3, 3) and the directrix y = 7 given, note that the vertex is usually between the focus and the directrix.

So, the vertex will have the same x-coordinate as the focus, which is -3, and the y-coordinate of the vertex becomes

`\begin{gathered} (3+7)/(2) \\ that\text{ is 3 from the y-coordinate of the focus and 7 from the directrix} \\ y=7 \\ (3+7)/(2)=(10)/(2)=5 \end{gathered}`

Hence coordinate of the vertex is (-3, 5)

Now, equation of a parabola is given as

`\begin{gathered} (x-h)^2=4p(y-k) \\ where\text{ \lparen h, k\rparen is the coordinate of the vertex and p is the focal length} \\ y=k-p,\text{ so we have } \\ 7=5-p \\ p=5-7=-2 \end{gathered}`

So putting in the values of h, k and p into the equation, we have

`\begin{gathered} (x-h)^(2)=4p(y-k) \\ (x-(-3)^2=4(-2)(y-5) \\ (x+3)^2=-8(y-5) \\ -(1)/(8)(x+3)^2=y-5\text{ that is dividing through by -8} \\ making\text{ y the subject, we have } \\ y=-(1)/(8)(x+3)^2+5 \end{gathered}`

Hence the answer is

`y=-(1)/(8)(x+3)^(2)+5`