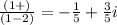Question

¨do you know what complex numbers are? Can you divide two complex numbers? Give us an example here!¨

Answer 1

A complex number z is a number of the form z = a + bi where a and b are real numbers, and i is the imaginary number, defined as the solution for i² = - 1.

We can indeed divide complex numbers. Let's take the numbers 1 + i and 1 - 2i for example. Dividing the first number by the second, we have

`(1+i)/(1-2i)`

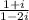
To solve this division, we need to multiply both the numerator and denominator by the complex conjugate of the denominator

`(1+\imaginaryI)/(1-2\imaginaryI)=(1+\imaginaryI)/(1-2\imaginaryI)\cdot(1+2i)/(1+2i)=((1+i)(1+2i))/((1-2i)(1+2i))`

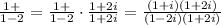
Expanding the products and solving the division, we have

`((1+\imaginaryI)(1+2\imaginaryI))/((1-2\imaginaryI)(1+2\imaginaryI))=(1+3i-2)/(1+4)=(-1+3i)/(5)=-(1)/(5)+(3)/(5)i`

And this is the result of our division

`((1+\imaginaryI))/((1-2\imaginaryI))=-(1)/(5)+(3)/(5)i`