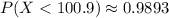Question

The mean life of a television set is 97 months with the variance of 169. If a sample of 59 televisions is randomly selected what is the probability that the sample mean would be less than 100.9 months? Round your answer to four decimal places if necessary

Answer 1

Given that the mean life of a television set is 97 months, you can set up that:

`\mu=97`

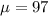
You also know that the variance is:

`\sigma^2=169`

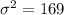
You can find the standard deviation by taking the square root of the variance. Then:

`\sigma=√(169)=13`

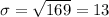
You need to find:

`P(X<100.9)`

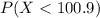
You need to find the z-score with this formula:

`z=\frac{\bar{X}-\mu}{(\sigma)/(√(n))}`

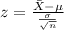
Knowing that:

`\bar{X}=100.9`

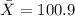
You can substitute values into the formula and evaluate:

`z=(100.9-97)/((13)/(√(59)))\approx2.30`

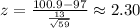
You have to find:

`P(z<2.30)`

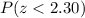
Using the Standard Normal Distribution Table, you get:

`P(z<2.30)\approx0.9893`

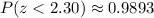
Then:

`P(X<100.9)\approx0.9893`

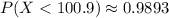
Hence, the answer is:

`P(X<100.9)\approx0.9893`