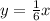Question

write an equation in slope intercept form of the line that passes through the given point and is perpendicular to the graph of the given equations(0,0); y = -6x+3y =

Answer 1

To find the equation of the line we need a point and the slope. We have the point but we need to find the slope, to do this we need to remember that two lines are perpendicular if and only if their slopes fullfils:

`m_1m_2=-1`

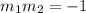
Now, the slope of the line given is -6, this comes from the fact that the line is written in the form y=mx+b, hence comparing both equation we conclude that.

Pluggin this value into the condition above we have:

`\begin{gathered} -6m_1=-1 \\ m_1=(-1)/(-6) \\ m_1=(1)/(6) \end{gathered}`

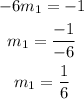
Therefore the slope of the line we are looking for is 1/6. The equation of a line is given as:

`y-y_1=m(x-x_1)`

Plugging the values of the slope and the point we have:

`\begin{gathered} y-0=(1)/(6)(x-0) \\ y=(1)/(6)x \end{gathered}`

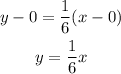
Therefore the equation we are looking for is:

`y=(1)/(6)x`