Question

Solve by completing the square. x2 - 8x + 5 = 0

Answer 1

`\begin{gathered} x_1=4+\sqrt[]{11} \\ x_2=4-\sqrt[]{11} \end{gathered}`

Explanation:

Solve the following quadratic completing the square:

`x^2-8x+5=0`

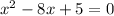
Keep x terms on the left and move the constant to the right side:

`x^2-8x=-5`

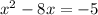
Then, take half of the x-term and square it.

`(-8\cdot(1)/(2))^2=16`

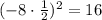
Now, add this result to both sides of the equation:

`x^2-8x+16=-5+16`

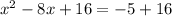
Rewrite the perfect square on the left.

`\begin{gathered} (x-4)^2=-5+16 \\ (x-4)^2=11 \end{gathered}`

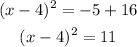
Take the square root of both sides:

`\begin{gathered} \sqrt[]{(x-4)^2}=\pm\sqrt[]{11} \\ x-4=\pm\sqrt[]{11} \\ x=\pm\sqrt[]{11}+4 \end{gathered}`

Hence, the two solutions of the equation are:

`\begin{gathered} x_1=4+\sqrt[]{11} \\ x_2=4-\sqrt[]{11} \end{gathered}`