Let x be the amount invest at 8%
Let y be the amount invest at 16%
Paul has $50,000 to invest:
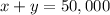
His intent is to earn 13% interest on his investment. He can invest part of his money at 8% interest and part at 16% interest.
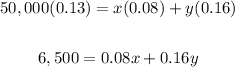
Use the next system of equations to find x and y:
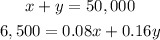
1. Solve x in the first equation:
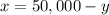
2. Substitute the x in the second equation by the value you get in the previous step:
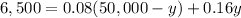
3. Solve y:
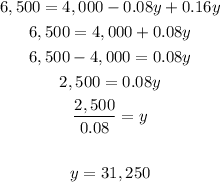
4. Use the value of y to solve x:
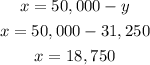
Solution for the system:
x=18,750
y=31,250
Answer: Paul needs to invers8% interest $18,75016% interest $31,250