Here, we have a special right triangle.
Let's solve for the variables, x and y.
Given:
common side = x
Hypotenuse of the larger triangle = 8
Let's find x using trigonometric ratio.
We have:
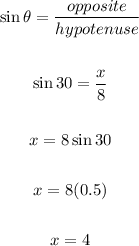
To solve for y, we have:

Solving further:
![\begin{gathered} y=\frac{4}{\sqrt[]{3}} \\ \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2e1uucbocc6kxn9m7jokeogt9kmuflz3p9.png)
Multiply both numerator and denominator by √3:
![\begin{gathered} y=\frac{4}{\sqrt[]{3}}\ast\frac{\sqrt[]{3}}{\sqrt[]{3}} \\ \\ y=\frac{4\sqrt[]{3}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zgndxeu1xsof85v8n65xhgs3tsd38cdmn1.png)
ANSWER:
![\begin{gathered} x=4 \\ \\ y=\frac{4\sqrt[]{3}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lyiiz0bsomg3vcangf37ycpunoj5d32r0s.png)