Question

One number is 22 more than another. Their product is – 121.Step 1 of 2: Set up an equation to solve the given word problem. Let x be the smaller number.Answer# KeypadKeyboard ShortcutsO x + x + 22 = - 121O x(22x) = - 121O x(x + 22)- 121O x(x – 22)- 121

Answer 1

Step 1

Let it be:

• x: The smaller number.

,

• x + 22: The larger number.

The product of both numbers is:

`x(x+22)`

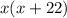
Since the product of both numbers is -121, we can write:

`x(x+22)=-121`

The word 'is' is represented by the symbol =.

Therefore, the equation to solve the given word problem is:

`x(x+22)=-121`Step 2

To find the numbers, we solve the previous equation.

`\begin{gathered} x(x+22)=-121 \\ \text{ Apply the distributive property on the left side} \\ x\cdot x+22\cdot x=-121 \\ x^2+22x=-121 \\ \text{ Add }121\text{ from both sides} \\ x^2+22x+121=-121+121 \\ x^2+22x+121=0 \end{gathered}`

Now, we can factor the expression on the left side using the perfect square trinomial rule.

`a^2+2ab+b^2=(a+b)^2`

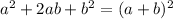
Then, we have:

`\begin{gathered} x^2+22x+121=0 \\ x^2+2\cdot11\cdot x+11^2=0 \\ (x+11)^2=0 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{(x+11)^2}=\sqrt[]{0} \\ x+11=0 \\ \text{ Subtract 11 from both sides} \\ x+11-11=0-11 \\ x=-11 \end{gathered}`

Finally, we find the another number.

`\begin{gathered} x+22=-11+22 \\ x+22=11 \end{gathered}`

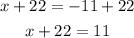
Therefore, the numbers are -11 and 11.