Step 1:
Concept: Calculate the area of each face and add all together to get the surface area of the pyramid.
The regular pyramid below have 4 triangles and a square
Step 2: Apply the area formula to find the area of the 4 triangles and a square.
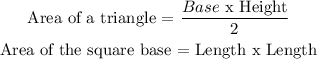
Step 3:
Given data for the triangle
Height = 21
Base = 12
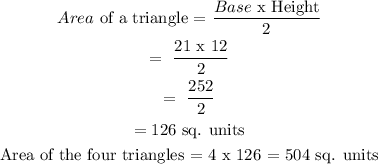
Step 4: Find the area of the square
Given data for the square
Length = 12
Area = length x length = 12 x 12 = 144 sq. units
Step 5: Add the area of the four triangles and the square.
Surface area of the regular pyramid = 504 + 144
= 648 sq. units