From the question,
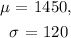
a. We are to find the probability that a single student randomly chosen from all those taking the test scores 1500 or higher?
we will do this using
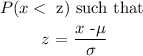
From the question, x = 1500.
Therefore
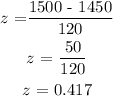
applying z - test
![\begin{gathered} P(x<strong>Thus, the probability that a single student is randomly chosen from all those taking the test scores 1500 or higher is approximately 34%</strong><p></p><p></p><p>b. From the question</p>[tex]\begin{gathered} n\text{ = 50, }^{}\text{ }\mu\text{ = 1450} \\ \bar{x}\text{ = 1470},\text{ }\sigma\text{ = 120} \end{gathered}]()
we will be using
![\begin{gathered} z\text{ = }\frac{\bar{x}\text{ - }\mu}{\frac{\sigma}{\sqrt[]{n}}} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v695m7bq13izkbr4jnuz3mvzyolxi3baqs.png)
inserting values
![\begin{gathered} z\text{ = }\frac{1470\text{ - 1450}}{\frac{120}{\sqrt[]{50}}} \\ z\text{ = }20\text{ }*\frac{\sqrt[]{50}}{120} \\ z\text{ = }\frac{\sqrt[]{50}}{6} \\ z\text{ = 1.18} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p9qfla7tin0ewjj0225pxawbwv5pu8mwwp.png)
Applying z-test
[tex]\begin{gathered} P(x
Hence,
The probability that the sample mean score of these students is 1470 or higher is approximately 12%