In this problem
we have that
sin(theta) is positive and cos(theta) is negative
That means
the angle theta lies on the II quadrant
Remember that
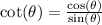
Find out the value of cos(theta)
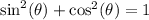
substitute the given value
![(\frac{\sqrt[]{48}}{8})^2+\cos ^2(\theta)=1](https://img.qammunity.org/2023/formulas/mathematics/college/829w7jtaro37b5j5i98i06dkki2llkf3e5.png)
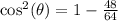
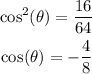
Find out the value of cot(theta)
substitute given values
![\cot (\theta)=-\frac{4}{\sqrt[\square]{48}}](https://img.qammunity.org/2023/formulas/mathematics/college/iuek7r7stmc6jjezncdm45q4dw0i12d7wo.png)
simplify
![\cot (\theta)=-\frac{4}{\sqrt[\square]{48}}\cdot\frac{\sqrt[]{48}}{\sqrt[]{48}}=-\frac{4\sqrt[]{48}}{48}=-\frac{\sqrt[]{48}}{12}=-\frac{4\sqrt[]{3}}{12}=-\frac{\sqrt[]{3}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/aamo3jz696k0kmcilbbp90ne943l3tap08.png)
Find out the angle theta
using a calculator
angle in II quadrant
theta=120 degrees
Convert to radians ---->