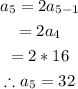Answer:
a1 = 2, a2 = 4, a3 = 8, a4 = 16, and a5 = 32
Step-by-step explanation:
Given the first term and the nth term of the sequence as;
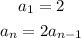
Since the first term is given already to be 2, let's go ahead and find the 2nd term;
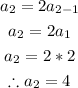
The 3rd term will be;
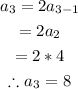
The 4th term can be found as follows;
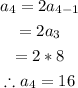
The 5th term can found as follows;