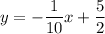1 Answer

Emiguevara · Answer 1 · 2023-11-03T03:05:23+0000

Step 1

Given; What is the equation of the line that passes through (5, 2) and is

perpendicular to y =

10x + 7?

Step 2

The slope of the given line is;

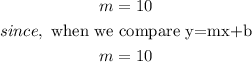
$\begin{gathered} m=10 \\ since,\text{ when we compare y=mx+b} \\ m=10 \end{gathered}$

Slope of perpendicular lines have the following relationship;

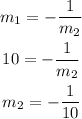
$\begin{gathered} m_1=-(1)/(m_2) \\ 10=-(1)/(m_2) \\ m_2=-(1)/(10) \end{gathered}$

Therefore the required equation will be in the form of;

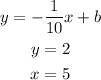
$\begin{gathered} y=-(1)/(10)x+b \\ y=2 \\ x=5 \end{gathered}$

Find b, the y-intercept

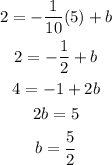
$\begin{gathered} 2=-(1)/(10)(5)+b \\ 2=-(1)/(2)+b \\ 4=-1+2b \\ 2b=5 \\ b=(5)/(2) \end{gathered}$

Thus the answer will be; Option B

$\begin{gathered} y=-(1)/(10)x+(5)/(2) \\ \\ \\ \\ \end{gathered}$

Please log in or register to add a comment.