Question

QUESTION 6 1 POINTA 20-foot string of lights will be attached to the top of a 12-foot pole for a holiday display. How far from the base of the poleshould the end of the string of lights be anchored?20 AProvide your answer below:ftFEEDBACK+O

Answer 1

Step-by-step explanation

Since we have the given sides, we can apply the Pythagorean Theorem in order to obtain the needed distance:

`Hypotenuse^2=Larger\text{ side}^2+Smaller\text{ side}^2`

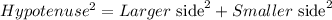
Plugging in the terms into the expression:

`20^2=Larger\text{ side\textasciicircum2+12}^2`

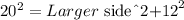
Subtracting 12^2 to both sides:

`20^2-12^2=Larger\text{ side}^2`

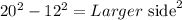
Computing the powers:

`400-144=Larger\text{ side}^2`

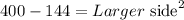
Subtracting numbers:

`256=Larger\text{ side}^2`

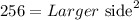
Applying the square root to both sides:

`√(256)=Larger\text{ side}`

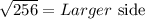
Computing the root:

`16=Larger\text{ side}`

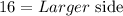
Switching sides:

`Larger\text{ side =16}`

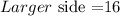
In conclusion, the solution is 16ft