1 Answer

Dangeroushobo · Answer 1 · 2023-12-28T15:59:11+0000

The card deck is a standard deck of 52 cards, with 13 cards in each suit.

For the experiment carried out by Michelle, we have the following information:

n(Spades) = 9

n(Hearts) = 11

n(Clubs) = 7

n(Diamonds) = 3

The total number of times she performed the experiment is

$n(\text{Total) = 9+11+7+3 = 30}$

The empirical probability will make use of the experimental results, while the theoretical probability will make use of the total possibilities.

PART A: Empirical Probability of selecting a heart.

Probability is calculated by

$P(\text{outcome) = }(n(outcome))/(n(total))$

Therefore, the probability is calculated as

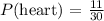
$P(\text{heart) = }(11)/(30)$

PART B: Theoretical probability of selecting a heart.

This is calculated by

$\begin{gathered} P(\text{heart) = }(13)/(52) \\ P(\text{heart) = }(1)/(4) \end{gathered}$

PART C: Empirical probability of selecting a club or diamond.

To calculate the probability for two outcomes, A or B, the probability can be calculated by

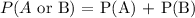
$P(A\text{ or B) = P(A) + P(B)}$

Therefore, we will find the probability of getting a club and then a diamond.

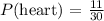
$P(\text{heart) = }(11)/(30)$
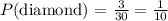
$P(\text{diamond) = }(3)/(30)=(1)/(10)$

Therefore, the probability of selecting a club or a diamond is

$\begin{gathered} P(\text{heart or diamond) = }(11)/(30)+(1)/(10) \\ P(\text{heart or diamond) = }(7)/(15) \end{gathered}$

PART D: Theoretical probability of selecting a club or a diamond

We will find the probability of getting a club and then a diamond.

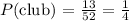
$P(\text{club) = }(13)/(52)=(1)/(4)$
$P(\text{diamond) = }(13)/(52)=(1)/(4)$

Therefore, the probability of selecting a club or a diamond is

$\begin{gathered} P(\text{heart or diamond) = }(1)/(4)+(1)/(4) \\ P(\text{heart or diamond) = }(1)/(2) \end{gathered}$

Please log in or register to add a comment.