Given:
SR = 26 m.
To find:
The area of shaded region.
Solution:
Here, QR ~ PS. So, angle PTS = angle QTR.
So, angle PTS = 73 degrees.
To find the area of the shaded region, we have to subtract the area of unshaded region from the area of the circle.
Here, SR is the diameter and SR = 26. So, the radius of the circle is 13 m.
Since, the unshaded regions are similar to each other. So, the total area of the unshaded region is:
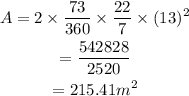
The area of the circle is:
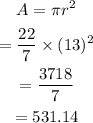
So, the area of shaded region is:
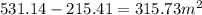
Thus, the area of the shaded region is 315.73 m^2.