Question

Find the solution set of each linear system3x+2y+z=8x+y+2z= 44x+y+z= y

Answer 1

x=0, y=4 and z=0.

Step-by-step explanation:

Given the system of linear equations:

`\begin{gathered} 3x+2y+z=8 \\ x+y+2z=4 \\ 4x+y+z=y \end{gathered}`

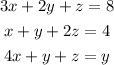
From the third equation:

`\begin{gathered} 4x+y-y+z=0 \\ 4x+z=0 \\ z=-4x \end{gathered}`

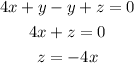
Substitute z=-4x into the first and second equations.

`\begin{gathered} 3x+2y-4x=8 \\ -x+2y=8 \\ \text{Second Equation} \\ x+y+2z=4 \\ x+y+2(-4x)=4 \\ x+y-8x=4 \\ -7x+y=4 \end{gathered}`

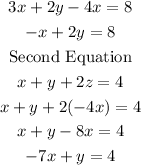
Solve the two results simultaneously.

`\begin{gathered} -x+2y=8\implies x=2y-8 \\ -7x+y=4 \\ -7(2y-8)+y=4 \\ -14y+56+y=4 \\ -13y=4-56 \\ -13y=-52 \\ y=-(52)/(-13) \\ y=4 \end{gathered}`

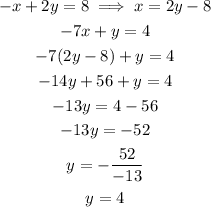
Substitute y=4 to solve for x.

`\begin{gathered} -7x+y=4 \\ -7x+4=4 \\ -7x=4-4 \\ -7x=0 \\ x=0 \end{gathered}`

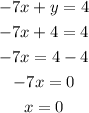
Finally, recall that: z=-4x

`z=-4(0)=0`

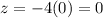
Therefore x=0, y=4 and z=0.