The equation of a line is the form of

The equation of the line was, however, given as
To rewrite this equation in slope-intercept form, we must first find the slope and y-intercept from the equation by rearranging it
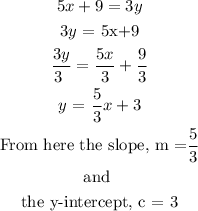
Hence the required equation is y =(5/3)x +3. The answer is the third option