we have three figures, we must find the area of each one and at the end, add them
lower triangle
we must find x and y to calculate the area, we will use trigonometric ratios
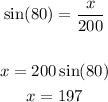
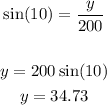
now calculate the area
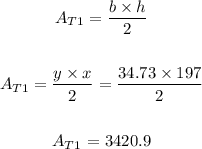
the area of the triangle is 3420.9 square feet
Rectangle
we have the height (160ft) and the base we calculate it in the previous step (x=197ft)
the area is
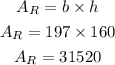
the area of the rectangle is 31520 square feet
Left Triangle
we must use trigonometric ratios to calculate Z
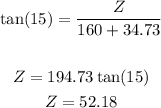
and the area of the triangle is
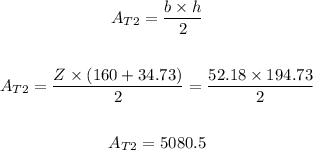
Total area
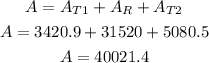
the total area is 40,021.4 square feet