Given:
• Perimeter of the rectangle = 24 inches
,
• The length is 3 inches greater than it's width.
Let's find the dimensions of the rectangle.
To find the dimensions, apply the formula for perimeter of a rectangle:
P = 2l + 2w
Where l is the length and w is the width.
Given that the length is 3 inches greater than the width, the length can be expressed as:
l = (w + 3) inches
Substitute 24 for P and (w + 3) for l in the formula:
P = 2l + 2w
24 = 2(w + 3) + 2w
Let's solve the equation for w:
24 = 2(w + 3) + 2w
APply distributive property:
24 = 2(w) + 2(3) + 2w
24 = 2w + 6 + 2w
Combine like terms:
24 = 2w + 2w + 6
24 = 4w + 6
Subtract 6 from both sides:
24 -6 = 4w + 6 - 6
18 = 4w
Divide both sides by 4:
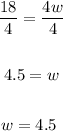
The width of the rectangle is 4.5 inches.
Since the lengh is 3 inches greater than the width, add 3 to 4.5 inches to get the length of the rectangle.
l = w + 3
l = 4.5 + 3
l = 7.5
The length of the rectangle is 7.5 inches.
Therefore, the dimensions of the rectangle are:
Length = 7.5 inches
Width = 4.5 inches
ANSWER:
Length = 7.5 inches
Width = 4.5 inches