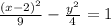Question

Hi! I have a question and I don't understand it's answer. Could you help me?It's in the attachment below.

Answer 1

To solve this question, we just need to evaluate our set of points in the standard form equation of a Hyperbola, and find the coefficients. This will give to us the equation for our Hyperbola. The standard form is

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

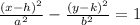
Let's start with the easier points, the x-intercepts (5, 0) and (-1, 0).

Since this hyperbola has two x-intercepts, we're dealing with a horizontal hyperbola, and the center is the midpoint between the x-intercepts.

`\begin{gathered} \bar{x}=(x_1+x_2)/(2)=(-1+5)/(2)=2 \\ \bar{y}=(y_1+y_2)/(2)=(0+0)/(2)=0 \end{gathered}`

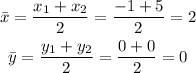
The center coordinates are (2, 0), then, our equation is

`((x-2)^2)/(a^2)-(y^2)/(b^2)=1`

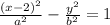
To find the missing coefficients, we can just substitute the remaining points and solve the system for a and b. Our final equation is

`\frac{(x-2)^2}{9^{}}-(y^2)/(4)^{}=1`