Answer:
Associative and commutative properties of addition
Explanation:
The one thing that the associative property of addition says that

and the commutative property of addition says
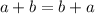
(the order of addition does not matter )
Now, the steps we take to solve our equation are the following:
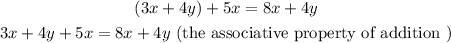
The second step is
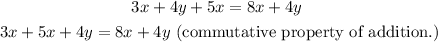
which simplifies to
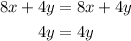
Hence, we used associative and commutative properties of addition to solve our equation.