Given the polynomials, let's simplify the polynomials and label them.
Polynomial 1:
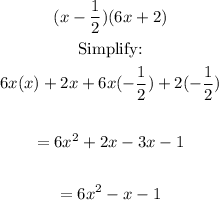
After simplifying, we have the simplified form:
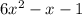
Since the highest degree is 2, this is a quadratic polynomial.
It has 3 terms, therefore by number of terms it is a trinomial.
Polynomial 2:
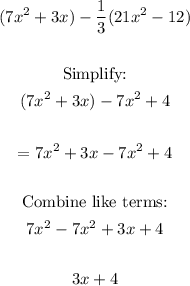
Simplified form:
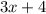
The highest degree is 1, therefore it is linear
It has 2 terms, therefore by number of terms it is a binomial
Polynomial 3:
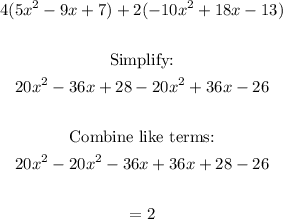
Simplified form:
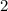
The highest degree is 0 since it has no variable, therefore it is a constant.
It has 1 term, by number of terms it is a monomial.
ANSWER:
Polynomial Simplified form Name by degree Name by nos. of ter
1 6x²-x-1 quadratic Trinomial
2 3x + 4 Linear Binomial
3 2 Constant Monomial