Question

Create a scatterplot using the following data relating the number of cigarettes a day smoked by a parent and thenumber of days the child missed school in the last quarter of the school year. Draw your estimate of the line of best fit.Select and give the coordinates of two points on the line. Find the slope of the line you drew. Write a sentence thatsummarizes the relationship between the two variables.

Answer 1

The equation for the line of best fit is given by:

y = mx + b

In which m is the slope

They are given by:

`m=\frac{n\sum^{}_{}xy-\sum^{}_{}x\sum^{}_{}y}{n\sum^{}_{}x^2-(\sum^{}_{}x)^2}`
`b=\frac{\sum^{}_{}y-m\sum^{}_{}x}{n}`

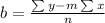
Sum of x:

Sum of all values of x.

`\sum ^{}_{}x=3\ast0+5+10+12+15+16+2\ast24+28+30+21+36_{}`
`\sum ^{}_{}x=221`

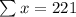
Sum of y:

`\sum ^{}_{}y=0+2\ast2+3+2\ast5+2\ast8+10+2\ast12+2\ast15+20`
`\sum ^{}_{}y=117`

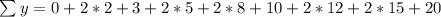
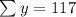
Sum of squares of x:

`\sum ^{}_{}x^2=3\ast0^2+5^2+10^2+12^2+15^2+16^2+2\ast24^2+28^2+30^2+21^2+36^2_{}`
`\sum ^{}_{}x^2=5323`

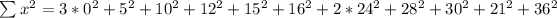
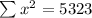
Sum of xy:

`\sum ^(\infty)_(n\mathop=0)xy=0\ast(0+2+5)+5\ast3+10\ast5+12\ast8+15\ast10+16\ast2`
`+24\ast(8+12)+28\ast15+30\ast15+21\ast20+36\ast12_{}`
`\sum ^{}_{}xy=2545`

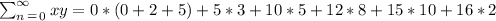
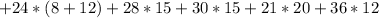
Slope:

14 students, so n = 14.

Then

`m=\frac{n\sum^{}_{}xy-\sum^{}_{}x\sum^{}_{}y}{n\sum^{}_{}x^2-(\sum^{}_{}x)^2}=(14\ast2545-(221\ast117))/(14\ast5323-221^2)=0.38`
`b=\frac{\sum^{}_{}y-m\sum^{}_{}x}{n}=(117-0.38\ast221)/(14)=2.36`

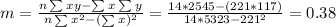
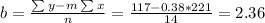
The line of best fit is y = 0.38x + 2.36. This means that for a parents that smokes x cigarettes a day, the child is expect to miss 0.38x + 2.36 days of school during the quarter.

Graphic