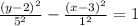Question

Rain equation of a hyperbola given the foci and the asymptotes

Answer 1

Step-by-step explanation

The equation for a hyperbola that opens up and down has the following general form:

`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`

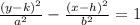
Where the foci of the hyperbola are located at (h,k+c) and (h,k-c) with c given by:

`c^2=a^2+b^2`

And asymptotes with slopes given by a/b and -a/b.

The hyperbola with the equation that we have to find has these two foci:

`(3,2-√(26))\text{ and }(3,2+√(26))`

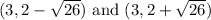
This means that:

`\begin{gathered} (h,k-c)=(3,2-√(26)) \\ (h,k+c)=(3,2+√(26)) \end{gathered}`

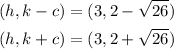
So we get h=3, k=2 and c=√26.

The slope of the asymptotes have to be 5 and -5 which means that:

`(a)/(b)=5`

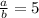
Using the value of c we have:

`c^2=26=a^2+b^2`

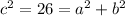
So we have two equation for a and b. We can take the first one and multiply b to both sides:

`\begin{gathered} (a)/(b)\cdot b=5b \\ a=5b \end{gathered}`

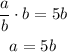
And we use this in the second equation:

`\begin{gathered} 26=(5b)^2+b^2=25b^2+b^2 \\ 26=26b^2 \end{gathered}`

We divide both sides by 26:

`\begin{gathered} (26)/(26)=(26b^2)/(26) \\ b^2=1 \end{gathered}`

Which implies that b=1. Then a is equal to:

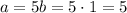
`a=5b=5\cdot1=5`Answer

Now that we have found a, b, h and k we can write the equation of the hyperbola. Then the answer is:

`((y-2)^2)/(5^2)-((x-3)^2)/(1^2)=1`