Question

Solve x2-12x + 11 = 0 by completing the square.

Answer 1

Given: A quadratic equation-

`x^2-12x+11=0`

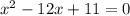
Required: To solve the equation by completing the square method.

Explanation: The general form of a quadratic equation is-

`ax^2+bx+c=0`

The given equation can be solved by the method of completing the square by adding and subtracting the term-

`((b)/(2))^2`

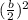
Hence, the given equation can be written as-

`x^2-12x+36-36+11=0`

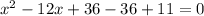
Now solving further as-

`\begin{gathered} x^2-2*6* x+6^2-25=0 \\ (x-6)^2=25 \\ (x-6)=√(25) \\ (x-6)=\pm5 \end{gathered}`

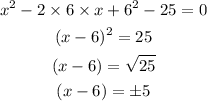
Thus,

`\begin{gathered} x-6=5\text{ or } \\ x-6=-5 \end{gathered}`

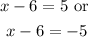
This gives-

`\begin{gathered} x=11\text{ or} \\ x=1 \end{gathered}`

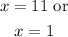
Final Answer: The solution to the equation is x=11 or x=1.