Question

Amplitude of damped oscillations reduces two folds during one second. Find the time of its five-fold decrease.

Answer 1

Answer:

The time for five-fold decrease = 2.32 seconds

Step-by-step explanation:

The final amplitude of a damped oscillation is given as:

`A=A_0e^(-kt)`

The amplitude reduces two-folds during one second

That is:

t = 1 second

A = 0.5A₀

`\begin{gathered} 0.5A_0=A_0e^(-kt) \\ (0.5A_0)/(A_0)=e^(-kt) \\ 0.5=e^(-k(1)) \\ 0.5=e^(-k) \\ \ln 0.5=-k \\ k=-\ln 0.5 \\ k=0.693 \end{gathered}`

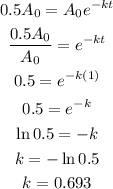
For a five-fold decrease

`\begin{gathered} (A_0)/(5)=A_0e^(-kt) \\ 0.2A_0=A_0e^(-kt) \\ (0.2A_0)/(A_0)=e^(-kt) \\ 0.2=e^(-kt) \\ \ln 0.2=-kt \\ \ln 0.2=-0.693t \\ -1.609=-0.693t \\ t=(-1.609)/(-0.693) \\ t=2.32 \end{gathered}`

The time for five-fold decrease = 2.32 seconds