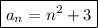Answer:
Explanation:
To find the nth term of a quadratic sequence, we need to determine the quadratic function that generates the sequence.
Given quadratic sequence:
4, 7, 12, 19, 28, ...
Begin by calculating the first differences between consecutive terms:
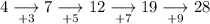
As the first differences are not the same, we need to calculate the second differences (the differences between the first differences):
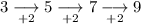
As the second differences are the same, the sequence is quadratic and will contain an n² term.
The coefficient of the n² term is half of the second difference.
As the second difference is 2, the coefficient of the n² term is 1.
Now we need to compare n² with the given sequence (where n is the position of the term in the sequence).

We can clearly see that the algebraic operation that takes n² to the terms of the sequence is add 3.
Therefore, the expression to find the the nth term of the given quadratic sequence is: